Charis Chrisna's Portfolio
Hi! My name is Charis Chrisna. I'm a hobbyist data scientist, using this site as a portfolio of my built projects and upcoming showcases.
Reach me out at:
charischrisna3@gmail.com
Source Code for Finite Element Analysis
Calculating I-Section Dimension
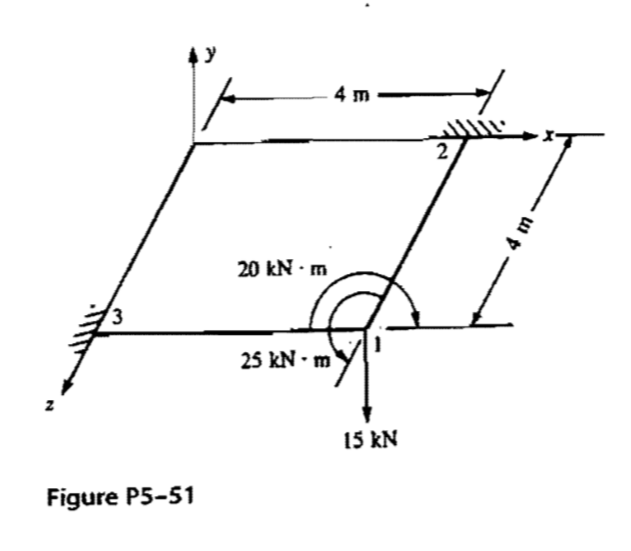
Part of a college assignment, fourth week of May 2020. For the grid P5-51, determine the nodal displacements and the local element forces.
Let:
- E = 210 GPa
- G = 84 GPa
- I = 2 * 10^-4 m^4
- J = 1 * 10^-4 m^4
- A = 1 * 10^-2 m^2
The formula for area moment of Inertia (I) for cross-sectional I-beams is as follows:
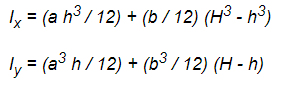
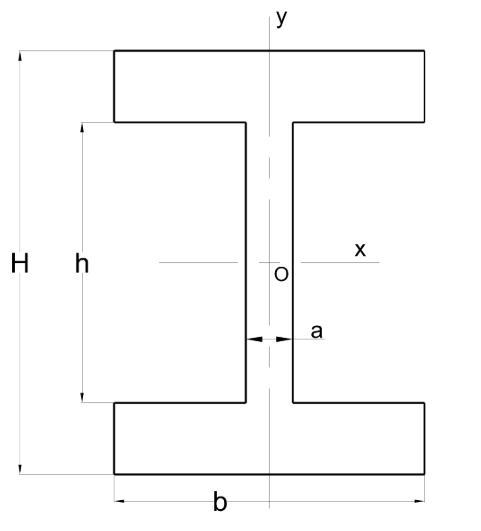
With:
 Credit: The Engineering Toolbox
Credit: The Engineering Toolbox
In which we cannot solve for the values of a, b, H, and h alone. h is defined as H - thickness. We may define thickness as c. Note that we are only solving with respect to the X axis, and not the Y axis.
Regarding this manner, we might iterate over the values of a, b , H and c with NumPy Arrays
Source code:
import numpy as np
points = np.arange(0.0, 20.0, 0.001)
for a in points:
for b in points:
for c in points:
for d in points:
num1 = b * (a**3)
denum1 = 12
num2 = ((b-d) / 2 ) * (a - ((2*c)**3))
denum2 = 12
form = num1/denum1 - (2*(num2/denum2))
form = round(form, 3)
if form < 0.00025 and form > 0.00015:
print(form)
print("with a = {0}, b = {1}, c = {2}, d = {3}".format(a,b,c,d))
print("---------------------------")
else:
pass
print("end")
Will print iterations within the nested loop. If the result is less than 0.00015 and more than 0.00025, the print prompt will not be executed. I found the closest value to the given area moment of inertia in this particular part of the iteration:
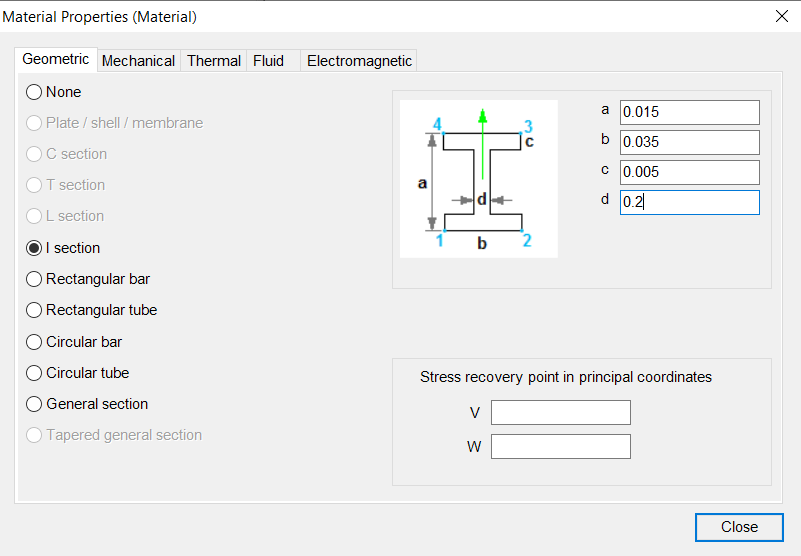
0.00020624
with a = 0.015, b = 0.035, c = 0.005, d = 0.2
---------------------------
*) Units are in metric metres, as specified in the problem above.
We then can conclude that the dimensions we’re looking for looks (roughly) like this: